When a metal or alloy is under a constant load or stress, it may undergo progressive plastic deformation over a period of time, even though applied stress is less than the yield strength at that temperaure. This time dependent strain is called creep (above definition is taken from AMIE study material) More information is taken from Wikipdeia and shown below.
In materials science, creep is the tendency of a solid material to slowly move or deform permanently under the influence of stresses. It occurs as a result of long term exposure to high levels of stress that are below the yield strength of the material. Creep is more severe in materials that are subjected to heat for long periods, and near melting point. Creep always increases with temperature.
The rate of this deformation is a function of the material properties, exposure time, exposure temperature and the applied structural load. Depending on the magnitude of the applied stress and its duration, the deformation may become so large that a component can no longer perform its function — for example creep of a turbine blade will cause the blade to contact the casing, resulting in the failure of the blade. Creep is usually of concern to engineers and metallurgists when evaluating components that operate under high stresses or high temperatures. Creep is a deformation mechanism that may or may not constitute a failure mode. Moderate creep in concrete is sometimes welcomed because it relieves tensile stresses that might otherwise lead to cracking.
In the initial stage, or primary creep, the strain rate is relatively high, but slows with increasing strain. This is due to work hardening. The strain rate eventually reaches a minimum and becomes near constant. This is due to the balance between work hardening and annealing (thermal softening). This stage is known as secondary or steady-state creep. This stage is the most understood. The characterized "creep strain rate" typically refers to the rate in this secondary stage. Stress dependence of this rate depends on the creep mechanism. In tertiary creep, the strain rate exponentially increases with strain because of necking phenomena.
General creep equation
where  is the creep strain, C is a constant dependent on the material and the particular creep mechanism, mb are exponents dependent on the creep mechanism, Q is the activation energy of the creep mechanism, σ is the applied stress, d is the grain size of the material, k is Boltzmann's constant, and T is the absolute temperature. and
is the creep strain, C is a constant dependent on the material and the particular creep mechanism, mb are exponents dependent on the creep mechanism, Q is the activation energy of the creep mechanism, σ is the applied stress, d is the grain size of the material, k is Boltzmann's constant, and T is the absolute temperature. and
 is the creep strain, C is a constant dependent on the material and the particular creep mechanism, mb are exponents dependent on the creep mechanism, Q is the activation energy of the creep mechanism, σ is the applied stress, d is the grain size of the material, k is Boltzmann's constant, and T is the absolute temperature. and
is the creep strain, C is a constant dependent on the material and the particular creep mechanism, mb are exponents dependent on the creep mechanism, Q is the activation energy of the creep mechanism, σ is the applied stress, d is the grain size of the material, k is Boltzmann's constant, and T is the absolute temperature. and Creep in materials must be taken into consideration before designing machine components which work in high temperature / high stress environments. Other components in which creep is important design consideration include Bulb filaments, Crown Glass, Metal Paper clips, ...
Don't forget to grab a copy of Material Science and Engineering book, which is essential for preparing for AMIE, Material Science.
with warm regards
AllMyPosts

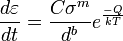






 (For sharp cracks)
(For sharp cracks)

