In crystallography, atomic packing factor (APF) or packing fraction is the fraction of volume in a crystal structure that is occupied by atoms. It is dimensionless and always less than unity. For practical purposes, the APF of a crystal structure is determined by assuming that atoms are rigid spheres. The radius of the spheres is taken to be the maximal value such that the atoms do not overlap. For one-component crystals (those that contain only one type of atom), the APF is represented mathematically by
where Natoms is the number of atoms in the unit cell, Vatom is the volume of an atom, and Vunit cell is the volume occupied by the unit cell. It can be proven mathematically that for one-component structures, the most dense arrangement of atoms has an APF of about 0.74. In reality, this number can be higher due to specific intermolecular factors. For multiple-component structures, the APF can exceed 0.74.
Worked out example
Body-centered cubic crystal structure
The primitive unit cell for the body-centered cubic (BCC) crystal structure contains nine atoms: one on each corner of the cube and one atom in the center. Because the volume of each corner atom is shared between adjacent cells, each BCC cell contains two atoms.
Each corner atom touches the center atom. A line that is drawn from one corner of the cube through the center and to the other corner passes through 4r, where r is the radius of an atom. By geometry, the length of the diagonal is a√3. Therefore, the length of each side of the BCC structure can be related to the radius of the atom by
Knowing this and the formula for the volume of a sphere((4 / 3)pi r3), it becomes possible to calculate the APF as follows:
-
-
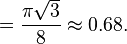 The above information is taken from Wikipedia. Please do refer to the same for further info.
The above information is taken from Wikipedia. Please do refer to the same for further info.
- with warm regards
- allmyposts
-
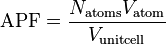



No comments:
Post a Comment